中学校で習う数学の範囲でアインシュタインの相対性理論を分かりやすく解説する

この記事は、中学の数学までの知識で相対性理論というものを断片的に、かつそこそこ本気のところまで理解したい！という方のためになるべく分かりやすく書いたページである。

対象は

①理系の高校生以上

②そこそこ数字に強い大学生以上

を想定している。

知識は中学の数学までしか使わないが、現象を理解するのはかなり難しいと思う。概略的な部分だけでも参考にしていただけたら嬉しい。

より簡単な、概要のみをイメージで知りたいという方は数式を使っていない

子どもに「相対性理論って何？」と聞かれたときのために概要を分かりやすく簡単に解説してみた - Yukihy Life

を見た方が良いかもしれない。

1.相対性理論とは？☆
2.必要な計算技術
3.相対論の要請と結果
4.現象をイメージするための動画☆
5.相対論の解説の準備
- 要請１　慣性系において、全ての物理法則は同じ形式で表される☆
- 要請２　光の速さは、どの慣性系から見ても変わらない
6.相対論の解説
7.[結果２　光の速さに近いスピードで動いているものは、止まっている人の世界から見ると時間が遅く流れる]
8.若返りたかったら24時間走り続けるというライフハック☆
- 相対論大好き天才A子さんのケース
  - プライベート
  - 彼女はどれくらい若返っていたのか
- 最強のお方Bさんのケース
  - プライベート
  - どれくらい若返っているのか
9.まとめ☆
10.参考図書☆
- 関連ページ

分かりやすく書いたつもりだが、技術不足で長い文章になってしまっている。

１～10まで見出しで分けであるが、忙しい人やとにかく内容だけ知りたいという方は

2.必要な計算技術

3.相対論の要請と結果

5.相対論の解説の準備

6.相対論の解説

のみを読んでいただければ理解していただけるようになっている。見なくても話がすすめられるところは(☆)をつけておいたので、どんどんスキップすることを推奨する。

また、結果だけ知りたいという方は、

3.相対論の要請と結果

の[結果]と[結果の解説と現象]のところだけ読んでいただいても良い。

1.相対性理論とは？☆

相対性理論とは、アインシュタインがほぼ一人で作り上げた新たな物理学分野で、特殊相対論と一般相対論とに分かれる。

名前からすると特殊相対論の方が難しそうだが、実際に勉強をすると一般相対論の方が数十倍難しい。

特殊相対論は東大などのハイレベル大学では教養課程で学ばれているものらしい。

つまり物理学を学んでいない人にとってもある程度は理解できる学問であるということだ。実際、アインシュタインの原文を訳した下の本

相対性理論 (岩波文庫)

作者: A.アインシュタイン,内山龍雄
出版社/メーカー: 岩波書店
発売日: 1988/11/16
メディア: 文庫
購入: 5人クリック: 79回
この商品を含むブログ (56件) を見る

これは三平方の法則さえ分かっていれば特殊相対論を理解することができるというものだ。

このページも一応、最小限の数学の知識で解説してある。

2.必要な計算技術

この記事では、計算技術として

基本的な方程式を解く技術
三平方の定理
ルートの計算

を使っている。だがこれらができなくても文章として読み進められるようにはしてある。

3.相対論の要請と結果

最初に、見通しをよくするために特殊相対性理論の要請と結果を書いてしまおうと思う。

要請

特殊相対論は、以下の二つの条件を要請とする。これらは後で再び解説をするのでとりあえず分からなくても進んで欲しい。

要請１　慣性系において、全ての物理法則は同じ形式で表される(特殊相対性原理)

要請２　光の速さは、どの慣性系から見ても変わらない(光速度普遍の原理)

慣性系…静止か、等速直線運動をしている世界のこと。

例えば僕たちがスタバの椅子に座って眺めている世界は慣性系の中の静止系という。

また等速で動いている電車の中の世界は慣性系の中の電車の系という。

イメージし辛い方は、「スタバの椅子から見える世界」と「等速で動く電車の椅子から見える世界」のことだと思えば良い

コラム　相対論で本質である慣性系について

「慣性系」「静止」ということを深く考えると特殊相対性原理が分かる【止まっているとは何なのか？】

結果

とりあえず上の二つの要請を認めると次のような現象が起きる。

結果１　光の速さに近いスピードで動いているものは、止まっている人から見ると縮んで見える

結果２　光の速さに近いスピードで動いているものは、止まっている人の世界から見ると時間が遅く流れる

結果３　質量とエネルギーとは等価なものである

結果の解説と現象

結果にひとつづつ説明を加えると

結果１　光の速さに近いスピードで動いているものは、止まっている人から見ると縮んで見える☆

いきなりトンデモ理論が現れたと思うかもしれないが、これも計算の結果から現れる現象である。

f:id:ftmaccho:20150119034140p:plain

文頭に「光の速さに近いスピードで動いているものは」と条件を付けているが、これは“目に見えるぐらいまで縮んで見えるには”光に近いスピードで動かなければいけないというだけで、光に近いスピードでなくとも動いているものというのは実は縮んでいるのだ（目の錯覚とかではなく）

Q&A地球から見て宇宙船が縮んでいるのなら、宇宙船から見て地球は伸びて見えるの？☆

答えは否

[宇宙船から見ても地球は縮んで見えます]

実際は宇宙船が動いていますが、宇宙船から見ると地球が動いて見える。すると上の図は、ちょうど宇宙船の中から地球を見ているような図になるはずだ。

すると同じことが起こり、今度は地球の方がが縮んで見える。宇宙船内部は縮んで見えません。

まとめると、地球から宇宙船は縮んで見えて、宇宙船から地球を見てもやはり縮んでみえるのです。(見えるというと錯視のようだが、そうでなく実際に縮む)

•コラム　ウサイン・ボルトに特殊相対論効果を加えるとこんなに細くなる(未完成)

結果２　光の速さに近いスピードで動いているものは、止まっている人の世界から見ると時間が遅く流れる

相対論の理論が今までなかなか生まれなかったのは、「時間の流れはみな同じ」という経験則に縛られていたからだ。その常識に疑問を持ったアインシュタインは本当にすごいと思う。

これも結果１と同じで、別に光の速さに近いスピードでなくとも、動いている人というのは時間はゆっくり流れているのだ。ただその誤差があまりにも小さすぎて僕たちは気づかないという訳である。

f:id:ftmaccho:20150119034214p:plain

Q&A上の右側の図で、宇宙船の中の人から見ると地球のが時間がたつのが早いってことですよね？☆

これも答えは否

[宇宙船の中から見ると、地球上の時間が遅れて見える]

これに関しては本当に混乱しそうだが、理由は上のと同じ。つまり地上から見ると動いているのは宇宙船だが、宇宙船の中から見ると動いているのは地球なのだ。

すると上の図が、宇宙船の内部から地球を見ているような図になる。手前の人は宇宙船に乗っていて、向こうに見える宇宙船を地球の絵にさしかえれば分かりやすい。

よって宇宙船から見ると地球がすごいスピードで動いていることになり、時間が遅れているのは地球の方である。

地球の時間と、宇宙船の時間は同じでなく、別々に流れていて、遅れているかどうかは「見る人がどちらか」というのに深く関わってくる。神のような存在により時間が「絶対的」に決まっている訳ではない。まさに「相対性」理論という訳だ。

それじゃ宇宙船の人が地球に帰ってきたとき、時間はどっちに合わせるの？という疑問は[コラム浦島効果&双子のパラドックス]で記事にする。[未完成です]

•コラム実例ミューオン(未完成)

•コラム実例カーナビ(未完成)

•コラム浦島効果＆双子のパラドックス（未完成）

結果３　質量とエネルギーは等価なものである☆

高校物理で、エネルギーと言うと運動エネルギーとか、位置エネルギーとかがある。これらは力学的エネルギーとまとめられ、例えば運動していなくて、位置も基準のところにすれば力学的エネルギーは０になる。

しかし相対性理論の計算をしていくと、その物体の質量そのものがエネルギーに変換される。その関係式はおなじみの　 $E=mc^2$ というものだ。 $E$ はエネルギー。 $m$ は質量。 $c$ は光速だ。

つまり質量のあるものが、その質量がなくなって全てエネルギーに変わるとこれくらいになるよという式だということ。

もう少し端的に説明をするならば、ある程度勉強した方なら、「質量保存則」と「エネルギー保存則」という言葉を聞いたことがあると思う。それぞれ、ある反応の前後で"質量"と"エネルギー"は、それぞれ保存されるという法則だ。

しかし、これらの法則は実は間違っていて、質量がエネルギーに変身することもあり、逆にエネルギーが質量に変身することもあるのだ。つまり「質量」と「エネルギー」は、それぞれ保存されるものではなく、「質量＋エネルギー」ではじめて保存されるものだったということである*2。

その実例は、実は原爆や原発など、非常に身近な部分に応用されている。

コラム　実例　原子力発電

相対論と原発・原爆の仕組み「HIROSHIMA・NAGASAKI・FUKUSHIMA」とアインシュタインが望んだ世界

この記事を読んでで分かること

この記事では、[要請２]の光速度不変の原理を使って、[結果２]の“時間のずれ”について説明する。時間がみな一定でないというのは衝撃的だし興味を持ってもらえると思い、また解説が比較的楽だからだ。

この記事を読み終えた段階で、もう少し数式をいじれば実は[結果１]の“距離の縮み”が説明できるが、それはコラムとして後日アップするこことにする。

また残念ながら、中学の知識のみでは[結果３]の質量と“エネルギーの等価性”については説明できない。

ここまでの知識での概略☆

相対性理論がなぜ相対性理論という名前なのかは、結果１や結果２のように、今まで「絶対的」だと思われていた「距離」や「時間」というものが人によって見え方がかわる。つまり「相対的」なものだとしたからである。

このページの頭で、相対性理論というのはほとんどがアインシュタインが独自に作り上げたと言ったが、実は相対性理論の元となる理論というのはほとんどできていたのだ。

ただその元となる理論を、他の物理学者たちは距離や時間を「絶対的」なものだと考えていたので相対性理論を作り上げることができなかった。アインシュタインはこれらの元の理論に、柔軟な解釈を加えることで新たな理論を作り上げたということだ。

•コラム　どのようにして特殊相対論という理論ができたのか(未完成)

そういった意味で「アインシュタインは人の理論をパクっただけじゃないか！」と批判をする人がいるがそれはお門違いである。コロンブスの卵と同じでこういった「人と違った視点を持てる人」ということが天才であり、また一般相対論まで体系化したのはほぼアインシュタインのみの力によるものだからだ。

4.現象をイメージするための動画☆

これらをイメージで表している動画があるので、参考として載せておく。ジャスト5分からアインシュタインランドという相対論の効果を極端に取り入れるた世界があり、上の結果のイメージをつくるのに役立つ。

アインシュタイン相対性理論第1回 part1 - YouTube

ちなみにこの動画内でも出てくるが、「空間が歪む」という現象は特殊相対論でなく一般相対論の内容となるので今回は割愛する。

5.相対論の解説の準備

いよいよ相対論の解説に入る。まずは２つの要請を簡単に解説し、その後ある現象を考え、それをいじくりまわして結論に持っていくというやり方でいこうと思う。

要請１　慣性系において、全ての物理法則は同じ形式で表される☆

要請の１つ目だが実は中学レベルで相対論を解説する場合はスキップ可だ。全く使わないといえば嘘になるが、以下の内容は興味がある人だけ読んでもらえれば良と思う。

まず、もう一度慣性系について書いておくと、

慣性系…静止か、等速直線運動をしている世界のこと。

例えば僕たちがスタバの椅子に座って眺めている世界は慣性系の中の静止系という。

また等速で動いている電車の中の世界は慣性系の中の電車の系という。

つまり要請の「慣性系において」というのは、「僕たちがスタバの椅子に座って回りを眺めている世界」と、「等速で運動する電車の椅子に座っている世界」を考えてくれれば良い。

これら二つは、片方は止まっていて片方は動いているのだが、両者の物理法則は同じであるということだ。

例えばスタバで上に投げたボールというのはそのまま自分の手元に落ちてくる。また等速の電車の中で上にボールを投げても、電車の中の投げた人から見ればボールはやはり手元に落ちてくる。

こういった簡単な例からも、両者の物理法則は同じと言える。

極端なことを言えば電車の中でも、電車が等速で動いている限り野球でもサッカーでも自由にできるわけだ。

しかし電車が動き出したり、止まるときは等速系でなく「加速系」になる[減速も、マイナスに加速と捉えます]「加速系」の中では体がぶれてとてもじゃないが野球はできない。

要請２　光の速さは、どの慣性系から見ても変わらない

こちらが非常に重要な要請である。要請１を読んでいない方のためにもう一度慣性系についての説明を加える

慣性系…静止か、等速直線運動をしている世界のこと。

例えば僕たちが椅子に座って眺めている世界は慣性系の中の静止系という。

また等速で動いている電車の中の世界は慣性系の中の電車の系という。

繰り返しになるが、要は「スタバの椅子から見える世界［静止系］と、「等速で動く電車の椅子から見える世界［等速度系］の２つのパターンを考えてくれれば良いということである。

これを元に要請２の文章を和文和訳すると、

「光の速さは、スタバの席から見ても、等速で動く電車の席から見ても変わらない」

ということになる。この文章で非日常的な疑問点が思いついていただけたであろうか。

もう少し解説をする。

光というのは凄く速い。なんせ１秒で30万kmも進んでしまうのだから。

スタバで座ってもしも光が通るのが見えたとしたら、それは30万km/時ですすんでいるだろう。

とある科学者が、光と一緒に旅をしたいと思い、光と同じ速さがでる電車を作ったとしよう。電車も30万km/時で進むという非リアルなことを考える。

その電車から乗って、30万km/時を維持し、同じスピードで進む光と旅ができるかと言ったらそれは否である。上の太文字文章から、スタバの席から見ても、電車の席から見ても、光の速さは30万km/時であるからだ。

まとめると同じ光を「動いていないスタバの席」から見ても、「30万km/時で走り続ける電車の中」から見ても、どちらも30万km/時で光が動いているように見えるのである。

f:id:ftmaccho:20150119034320p:plain

これが要請の言いたいことで、光速度不変の原理と呼ばれる。*4

この原理は「何で成り立つの？」と聞かれても答えられない。原理だから原理なのであり、理由はないのだ。ここにやたらと理由を求めることに意味はなく、とりあえずこの原理を認めると実用的な理論が出来上がるといったスタンスを持ってほしい。*5 *6

余談だがアインシュタインは、子どものころ「光」というものに興味を持ち、「光と旅をしたらどうなるのだろう」という夢をもったそうだ。

6.相対論の解説

いよいよ内容を解説していく

よくある状況を考える

ここからはアルファベットや数式が出てくるが、図を使ってできるだけ分かりやすくしているつもりなのでご了承願いたい。

ある宇宙船を考える。この宇宙船の中には人と光時計が入っている。光時計とは、図のように宇宙船の上と下とに鏡を貼り付けてて、その間を光が何度も折り返す。

f:id:ftmaccho:20150119045918p:plain

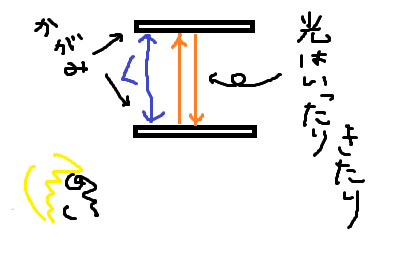
これが何回折り返したかの回数で時間を決めるというものだ。つまりは光を基準にした時計と考えてもらってよい。

図にあるように、鏡の間の距離を $L$ とする。

そして宇宙船は地球に対して $v$ の速度で、光の進む向きと直角方向に等速で動いているとする。*7

光の速さを $c$ とする。

宇宙船の中の人の時間を $t$ とし、地球上の人の時間を $t’$ とする。

しつこいが、ここで宇宙船の中の人の時間と、地球上の人の時間を同じにしないことで特殊相対論という理論ができる。逆に言えばここで両者の時間を同じ $t$ とすると、矛盾が生じてしまう。(詳しくは後述)

準備は整った！

とりあえずアルファベットが出たのでまとめておくと

$L$ 鏡の間の距離

$v$ 宇宙船の地球にたいする速度

$c$ 光速

$t$ 宇宙船の中の人の時間

$t'$ 地球の人の時間

実際に宇宙船を走らせてみよう！

まずは宇宙船の中の人の視点

f:id:ftmaccho:20150119050019p:plain

うん。うまく走ったみたい。ってかさっきと同じ図だ。

視点を変えて地球上の人から３枚写真をとったとしよう。

f:id:ftmaccho:20150119050204p:plain

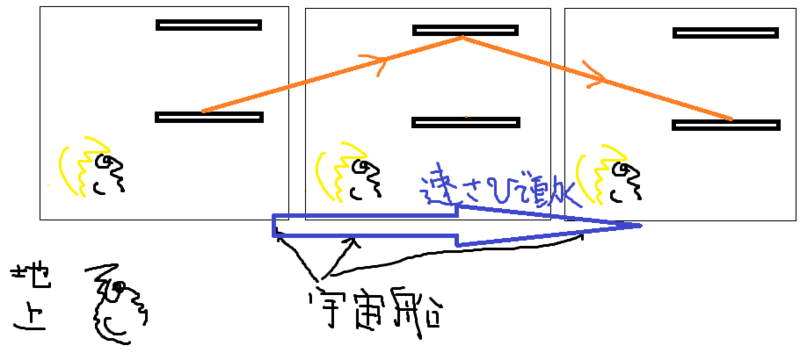
ここでは光が行って帰ってくるまでを図にした。

それぞれの視点で、光が行って帰ってくるまででの一往復で方程式を作ってみたい。作る方程式は(①光の通る距離)=(②光の速さ)×(③時間)という式だ。

宇宙船の中の人の視点から

しつこいようだが図をのせる

f:id:ftmaccho:20150119050019p:plain

①行って帰ってきているので(距離)は $2L$

②光の速さは誰から見ても $c$

③時間は仮定より $t$

よって方程式は

$2L=ct$

となる。便宜上式変形をして

$L= \frac{ct}{2} \tag{1}$

としておく。

ここまではおそらく問題はないと思う。

地球から見た視点

続いて地球から見る。こっちはちょっとややこしいので、図の説明から入る

f:id:ftmaccho:20150119050426p:plain

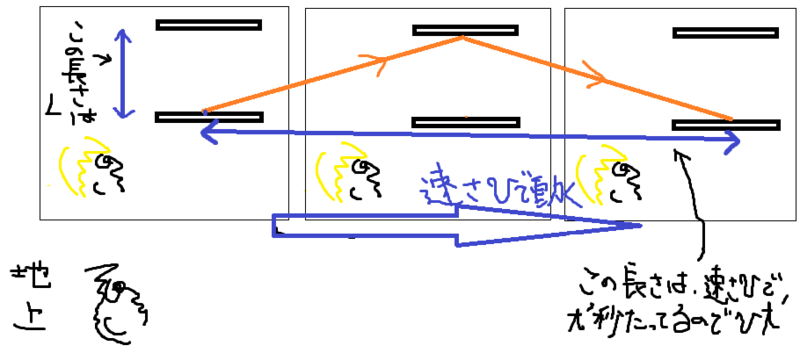
①まず、地球から見ると宇宙船は動いて見えるので、光は斜めに走っているように見える。そして光が横にどれだけ動くかは、[宇宙船の速さ]×[時間]となるので、 $vt'$ だ。よって光が通った距離(オレンジ部分)を求めるために、三平方の定理を使いたい。

そのために上の図をとりあえずシンプルにし

f:id:ftmaccho:20150119050646p:plain

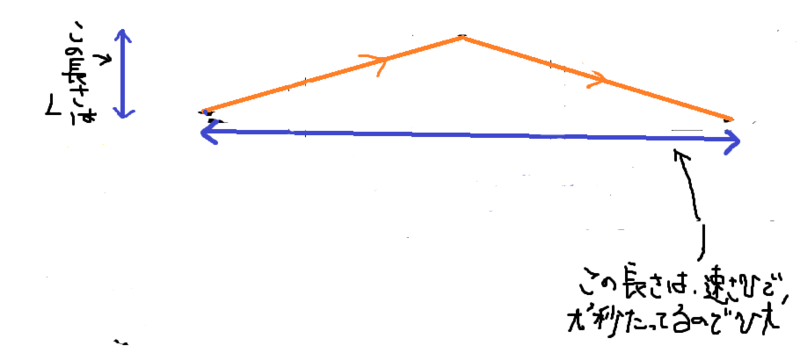
直角三角形に折りたたんでやる

f:id:ftmaccho:20150119050730p:plain

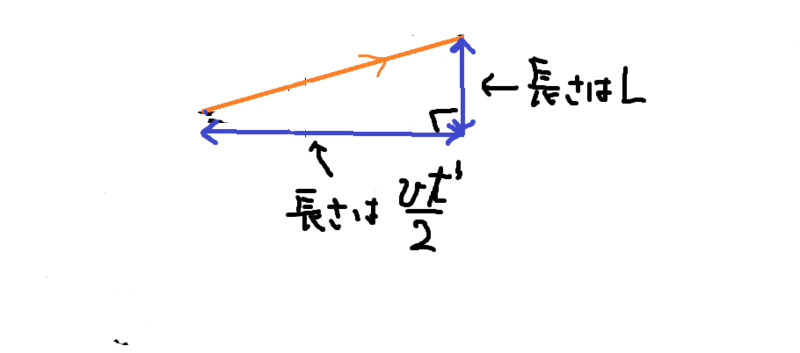
すると上のオレンジの部分は、三平方の定理より

$\sqrt{({ \frac{vt’}{2}})^{2}+L^{2}}$

となるので、光が通った距離はその２倍の

$2\sqrt{({ \frac{vt’}{2}})^{2}+L^{2}}$

となる。

②光の速さは誰から見ても $c$ (要請２からここが変わらないことに注意)

③時間は仮定より $t'$

よって方程式は

$2\sqrt{{( \frac{vt’}{2}})^{2}+L^{2}}=ct’$

となる。両辺を自乗すると

$4({(\frac{vt’}{2})}^{2}+L^{2})=c^{2}t’^{2}$

となるので、左辺を計算して

$v^{2}t’^{2}+4L^{2}=c^{2}t’^{2} \tag{2}$

となる。

クライマックス

もう少し計算すれば終わりだ。計算が嫌な人は結論を見てもらって良い。とにかく上の $(1)$ と $(2)$ ２つの方程式から $t$ と $t'$ の関係を見れば、時間が遅れているかどうかが分かる。

そこで上の２つの式から、 $(1)$ 式

$L= \frac{ct}{2} \tag{1}$

を $(2)$ 式

$v^{2}t’^{2}+4L^{2}=c^{2}t’^{2} \tag{2}$

に代入して $L$ を消去してみると

$v^{2}t’^{2}+4×\frac{c^{2}t^{2}}{4}=c^{2}t’^{2}$

となる。式をどんどいじくると

$v^{2}t’^{2}+c^{2}t^{2}= c^{2}t’^{2}$

$c^{2}t^{2}= c^{2}t’^{2}-v^{2}t’^{2}$

$c^{2}t^{2}= (c^{2}-v^{2})t’^{2}$

$t^{2}= \frac{1}{c^{2}}(c^{2}-v^{2})t’^{2}$

$t^{2}= (1- \frac{v^{2}}{c^{2}})t’^{2}$

$t=\sqrt{1- \frac{v^{2}}{c^{2}}}t’ \tag{3}$

となる。できた！この $(3)$ 式が時間の遅れを表す方程式である。[時間はプラスのみとった]

7.[結果２　光の速さに近いスピードで動いているものは、止まっている人の世界から見ると時間が遅く流れる]

出てきた方程式と、アルファベットの意味を整理する

$t=\sqrt{1- \frac{v^{2}}{c^{2}}}t' \tag{3}$

$t$ ：宇宙船の中の人の時間

$t'$ ：地球上の人の時間

$v$ ：宇宙船の速度

$c$ ：光速

である。使った仮定は、方程式を作ったときの②で書いたように光速度不変の原理だけだ。あとは三平方の定理とか、図を見たまんまを式にしただけである。これによって出された式の意味を考えてみる。

時間の流れを同じにすると

多くの物理学者が、時間の流れは絶対的なものと捉えていた。つまり宇宙船にのってようと地球上にいようと時間は同じと考えたのである。

上の式で言えば $t=t’$ ということだ。これを上の $(3)$ 式に代入すると

$t=\sqrt{1- \frac{v^{2}}{c^{2}}}t$

$1=\sqrt{1- \frac{v^{2}}{c^{2}}}$

となり、意味不明な方程式が出来上がってしまう。

この式が成り立つには $v=0$ でなければいけないからだ。

つまり光速度不変の原理を元にすると、時間のずれというのは自然と表れるものなのである。

相対論の効果が表れるのは

この $(3)$ 式

$t= \sqrt{1- \frac{v^{2}}{c^{2}}}t' \tag{3}$

で相対論の効果を表しているのはルートの部分だ。このルートの部分が無ければ、 $t=t’$ となり時間のずれがない。つまり相対論の効果がないということになる。

それではルートの中はというと、

$\sqrt{1- \frac{v^{2}}{c^{2}}}$ であり

$v$ : 宇宙船の速度

$c$ : 光速

である。 $c$ は値が決まっていて30万km/秒であるので、 $v$ がかなり大きくないと、ルートの中はほぼ１になって $t=t’$ となってしまう。

しかし実際、0.1 $c$ =3万km/秒も僕たちは出すことができないだろう。

時間のずれを僕たちが日常生活で感じることができないのは、このように光速に対して影響をがあるほど大きい速度を出すことができないからだ。

もしも超速く歩けるブーツが開発されたら☆

もし未来に光の速度の60%の速度で歩けるようになったとする。上までの「宇宙船」の部分を「ブーツを履く人」に代えれば良い。すなわち

$t= \sqrt{1- \frac{v^{2}}{c^{2}}}t' \tag{3}$

$t$ ：ブーツで歩いている人の時間

$t'$ ：止まっている人の時間

$v$ ：ブーツで歩いている人の速度

$c$ ：光速

となる。ブーツを履いている人は光の速度の60%で歩けるので $v=0.6c$ 。これを $(3)$ 式に代入すると、

$t= \sqrt{1- \frac{(0.6c)^{2}}{c^{2}}}t'$

$t= \sqrt{1- \frac{0.36c^{2}}{c^{2}}}t'$

$t= \sqrt{1- 0.36}t'$

$t= \sqrt{0.64}t'$

$t= 0.8t'$

$t$ ：ブーツで歩いている人の時間

$t'$ ：止まっている人の時間

なので、ブーツで歩いている人は、止まっている人よりも0.8倍の時間で進んでいることになり、遅れていることが分かる。*8

8.若返りたかったら24時間走り続けるというライフハック☆

若返り、それは世の全ての女性の憧れ。特殊相対論をつかって時間の流れを遅くして、永遠の美貌を手に入れるのよー！*9

相対論大好き天才A子さんのケース

プライベート

物心ついたときから相対論を勉強し、５歳でマスター
卒園式の発表はシュヴァルツシルト半径とブラックホールの地平線について
10歳での失恋を境にダイエットを始めたことで、一日18時間100m/秒で走り続ける
彼女は80歳で亡くなる直前まで失恋を引きづっていたという

彼女はどれくらい若返っていたのか

$v$ =100m/s $c$ =300000000m/s

彼女の走り続けた時間をを秒に直すと $t'$ =60s/m×60m/h×18h/d×365d/y×70y=1655640000秒

$(3)$ 式で $t$ を計算し、元の時間との差をとると、縮む時間は $9.2×10^{-5}$ 秒、つまり70年間で10万分の9.2秒縮ませることに成功した。

最強のお方Bさんのケース

プライベート

現在58歳 [多分]
田中邦衛さんによく似ていると言われる
移動は本気だしていないので光速の70％ぐらい
一日に推定10秒ぐらいは移動する？
「光の速さで蹴られたことはあるか～い？」

どれくらい若返っているのか

$v＝0.7c$

移動している時間を秒に直すと $t'$ =211700秒

同じく $(3)$ 式を使って計算をすると60516秒、約16時間縮ませることに成功。

9.まとめ☆

相対論は、上に計算をしたように、僕たちの生活にはほぼ効果として表れてこないので、日常的に感じることはない。式を見てもらえば分かるが、結局相対論的に効果がでるのは、光速に近いぐらいで動かなければいけないからだ。

しかし宇宙空間に関わることや、粒子レベルの話になると相対論の効果というのは如実に表れてくる。

相対論を利用することでタイムマシンは理論上できる。しかしそのためには、光速近くで動くロケットというものを開発する必要があり、技術が追い付いていないというのが現状だ。

相対性理論は、非日常的なことが起こりすぎていて、今でも認めずに反対している人は多い。というか相対論でググるとそういったページばかり出てくる…。

相対論を分かりやすく書いているページというのはありそうでなかったので僕自身未熟なことは分かっているが書いてみた。

コラムのページとかは今後増やしていこうと思う。

10.参考図書☆

図解相対性理論と量子論―物理の2大理論が1冊でわかる本

posted with ヨメレバ

佐藤勝彦 PHP研究所 2006-05

Amazon

Kindle

楽天ブックス

ぶっちゃけかなり分かりやすい。

相対性理論とタイムトラベル―キップ・ソーン博士が語る時空旅行 (ニュートンムック Newton別冊)

posted with ヨメレバ

水谷仁ニュートンプレス 2012-05-28

Amazon

楽天ブックス

図なんかはニュートンのものを参考にした。

理論電磁気学

posted with ヨメレバ

砂川重信紀伊國屋書店 1999-09

Amazon

楽天ブックス

運動物体の電磁気学の章がかなりおもしろい。

相対性理論 (物理テキストシリーズ 8)

posted with ヨメレバ

内山龍雄岩波書店 1987-01-29

Amazon

楽天ブックス

一般が全然読めてない…。頑張ります

その他啓蒙書から専門書までの相対論に関する本

<a href="http://www.yukihy.com/entry/book-theory-of-relatively" data-mce-href="http://www.yukihy.com/entry/book-theory-of-relatively">相対性理論に関して学べるおすすめ本!【一般向けの啓蒙書から専門書まで】 - Yukihy Life</a>www.yukihy.com